Mục lục
- Mục lục
- Giới thiệu
- Different parts of a JPEG
- Bắt đầu tập tin và kết thúc tập tin
- Mã hóa JPEG
- Không gian màu JPEG
- Biến đổi và lượng tử hóa cosine rời rạc
- Zig-zag
- Mã hóa độ dài chạy và Delta
- Huffman Encoding
- Giải mã JPEG
- Trích xuất bảng Huffman
- Giải mã bảng lượng tử hóa
- Giải mã bắt đầu khung
- Giải mã Bắt đầu quét
- Hiển thị hình ảnh trên màn hình
- Tổng kết
- Đọc thêm
Chào mọi người! 👋 Hôm nay chúng ta sẽ tìm hiểu thuật toán nén JPEG. Một điều mà nhiều người không biết là JPEG không phải là một định dạng mà là một thuật toán. Hình ảnh JPEG bạn nhìn thấy hầu hết ở định dạng JFIF (Định dạng trao đổi tệp JPEG) sử dụng nội bộ thuật toán nén JPEG. Đến cuối bài viết này, bạn sẽ hiểu rõ hơn nhiều về cách thuật toán JPEG nén dữ liệu và cách bạn có thể viết một số mã Python tùy chỉnh để giải nén nó. Chúng tôi sẽ không đề cập đến tất cả các sắc thái của định dạng JPEG (như quét lũy tiến) mà chỉ đề cập đến định dạng đường cơ sở cơ bản khi viết bộ giải mã của chúng tôi.
Giới thiệu
Tại sao phải viết một bài khác trên JPEG khi đã có hàng trăm bài viết trên internet? Chà, thông thường khi bạn đọc các bài viết về JPEG, tác giả chỉ cung cấp cho bạn thông tin chi tiết về định dạng trông như thế nào. Bạn không triển khai bất kỳ mã nào để thực hiện việc giải nén và giải mã thực tế. Ngay cả khi bạn viết mã, nó vẫn ở dạng C/C++ và không thể truy cập được đối với nhiều người. Tôi dự định thay đổi điều đó bằng cách chỉ cho bạn cách bộ giải mã JPEG cơ bản hoạt động bằng Python 3. Tôi sẽ dựa trên mã được cấp phép MIT này nhưng sẽ sửa đổi nhiều để tăng khả năng đọc và dễ hiểu. Bạn có thể tìm thấy mã đã sửa đổi cho bài viết này trên repo GitHub của tôi.
Different parts of a JPEG
Hãy bắt đầu với bức ảnh đẹp này của Ange Albertini. Nó liệt kê tất cả các phần khác nhau của một tệp JPEG đơn giản. Hãy nhìn vào nó. Chúng ta sẽ khám phá từng phân khúc. Bạn có thể phải tham khảo hình ảnh này khá nhiều lần khi đọc hướng dẫn này.
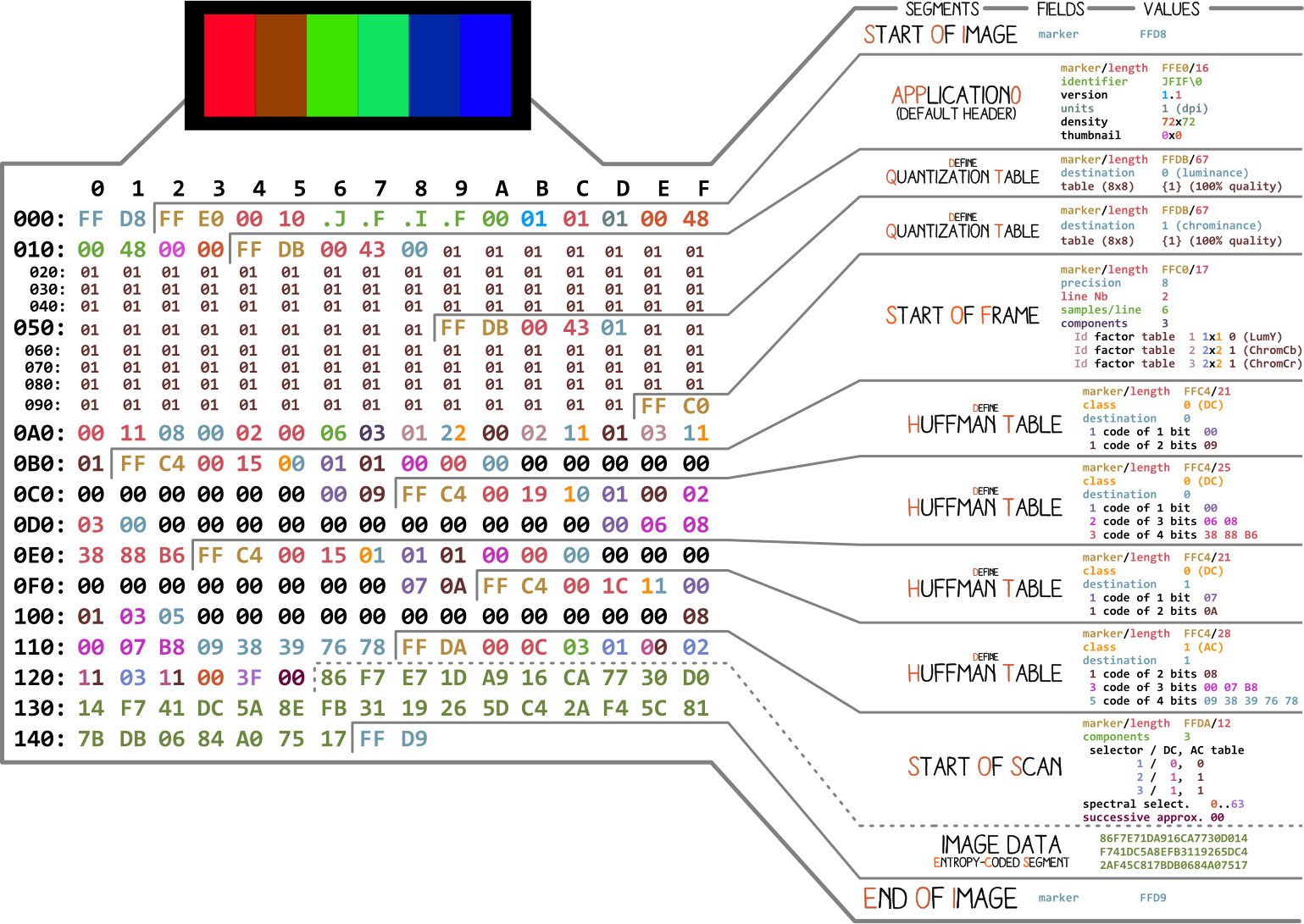
Ở mức rất cơ bản, hầu hết mọi tệp nhị phân đều chứa một vài điểm đánh dấu (hoặc tiêu đề). Bạn có thể coi những điểm đánh dấu này giống như dấu trang. Chúng rất quan trọng trong việc hiểu tệp và được các chương trình như tệp (trên Mac/Linux) sử dụng để cho chúng tôi biết chi tiết về tệp. Các điểm đánh dấu này xác định nơi lưu trữ một số thông tin cụ thể trong một tệp. Hầu hết các điểm đánh dấu được theo sau bởi thông tin độ dài length cho đoạn đánh dấu cụ thể. Điều này cho chúng ta biết đoạn cụ thể đó dài bao nhiêu.
Bắt đầu tập tin và kết thúc tập tin
Điểm đánh dấu đầu tiên chúng tôi quan tâm là FF D8. Nó cho chúng ta biết đây là điểm bắt đầu của hình ảnh. Nếu không thấy nó, chúng ta có thể cho rằng đây là một tập tin khác. Một điểm đánh dấu quan trọng không kém khác là FF D9. Nó cho chúng ta biết rằng chúng ta đã đến cuối tệp hình ảnh. Mỗi điểm đánh dấu, ngoại trừ FFD0 đến FFD9 và FF01, ngay sau đó là bộ xác định độ dài sẽ cung cấp cho bạn độ dài của đoạn đánh dấu đó. Đối với các điểm đánh dấu bắt đầu và kết thúc tệp hình ảnh, mỗi điểm sẽ luôn dài hai byte.
Trong suốt hướng dẫn này, chúng ta sẽ làm việc với hình ảnh này:

Hãy viết một số mã để xác định các điểm đánh dấu này.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Chúng tôi đang sử dụng struct để giải nén các byte dữ liệu hình ảnh. >H yêu cầu struct xử lý dữ liệu ở dạng big endian và thuộc loại unsigned short. Dữ liệu trong JPEG được lưu trữ ở định dạng big-endian. Chỉ dữ liệu EXIF có thể ở dạng endian nhỏ (mặc dù nó không phổ biến). Và một đoạn ngắn có kích thước 2 nên chúng tôi cung cấp giải nén hai byte từ img_data của chúng tôi. Bạn có thể tự hỏi làm sao chúng tôi biết đó là một đoạn ngắn. Chà, chúng ta biết rằng các điểm đánh dấu trong JPEG có 4 chữ số hex: ffd8. Một chữ số hex bằng 4 bit (1/2 byte) nên 4 chữ số hex sẽ bằng 2 byte và một chữ số ngắn bằng 2 byte.
Ngay sau phần Bắt đầu quét là dữ liệu quét hình ảnh và dữ liệu quét hình ảnh đó không có độ dài được chỉ định. Quá trình này tiếp tục cho đến khi tìm thấy điểm đánh dấu “cuối tập tin”, vì vậy hiện tại chúng tôi đang “tìm kiếm” thủ công điểm đánh dấu EOF bất cứ khi nào chúng tôi nhìn thấy điểm đánh dấu SOC.
Bây giờ chúng ta đã có khung cơ bản, hãy tiếp tục và tìm hiểu phần còn lại của dữ liệu hình ảnh chứa gì. Trước tiên chúng ta sẽ xem xét một số lý thuyết cần thiết và sau đó chuyển sang viết mã.
Mã hóa JPEG
Đầu tiên tôi sẽ giải thích một số khái niệm cơ bản và kỹ thuật mã hóa được JPEG sử dụng, sau đó việc giải mã sẽ tự nhiên diễn ra theo hướng ngược lại. Theo kinh nghiệm của tôi, việc trực tiếp cố gắng hiểu ý nghĩa của việc giải mã là hơi khó.
Mặc dù hình ảnh bên dưới hiện không có nhiều ý nghĩa đối với bạn nhưng nó sẽ cung cấp cho bạn một số điểm neo để bạn giữ vững trong khi chúng ta thực hiện toàn bộ quá trình mã hóa/giải mã. Nó hiển thị các bước liên quan đến quá trình mã hóa JPEG: (src)
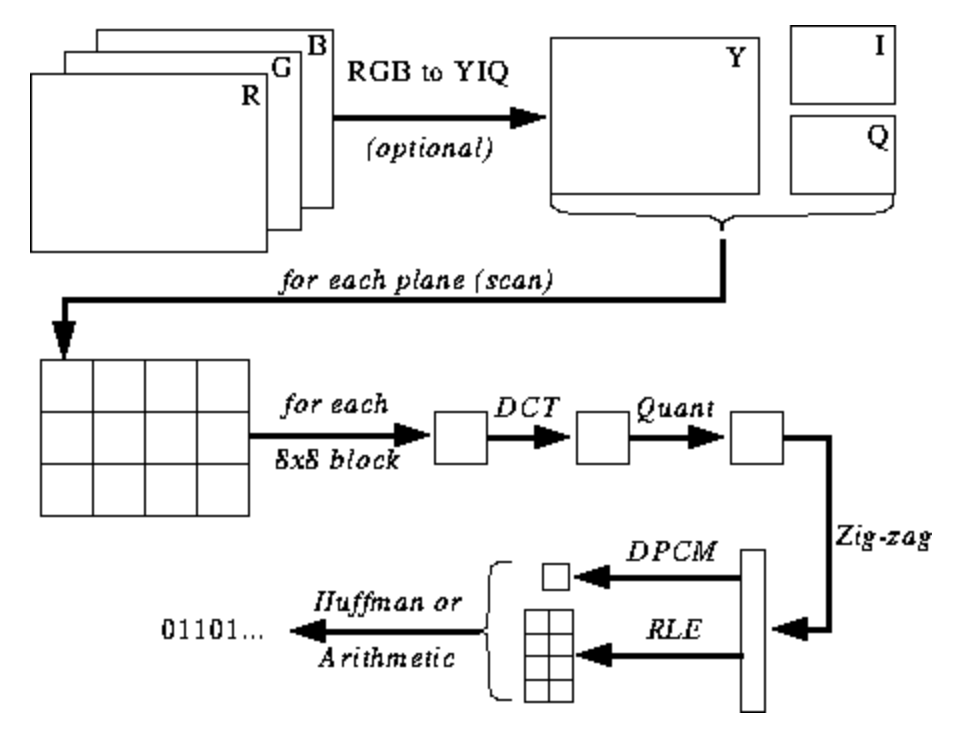
Không gian màu JPEG
Theo thông số JPEG (ISO/IEC 10918-6:2013 (E), mục 6.1):
- Hình ảnh được mã hóa chỉ có một thành phần được coi là dữ liệu thang độ xám trong đó 0 là màu đen và 255 là màu trắng.
Hình ảnh được mã hóa bằng ba thành phần được coi là dữ liệu RGB được mã hóa dưới dạng YCbCr trừ khi hình ảnh chứa đoạn đánh dấu APP14 như được chỉ định trong 6.5.3, trong trường hợp đó, mã hóa màu được coi là RGB hoặc YCbCr theo dữ liệu ứng dụng của điểm đánh dấu APP14 bộ phận. Mối quan hệ giữa RGB và YCbCr được xác định như được chỉ định trong Rec. ITU-T T.871 ISO/IEC 10918-5. - Hình ảnh được mã hóa với bốn thành phần được giả sử là CMYK, với (0,0,0,0) biểu thị màu trắng trừ khi hình ảnh chứa đoạn đánh dấu APP14 như được chỉ định trong 6.5.3, trong trường hợp đó mã hóa màu được coi là CMYK hoặc YCCK theo dữ liệu ứng dụng của đoạn đánh dấu APP14. Mối quan hệ giữa CMYK và YCCK được xác định như quy định tại Điều 7.
Hầu hết việc triển khai thuật toán JPEG đều sử dụng độ chói và sắc độ (mã hóa YUV) thay vì RGB. Điều này cực kỳ hữu ích trong JPEG vì mắt người khá kém trong việc nhìn thấy sự thay đổi độ sáng tần số cao trên một khu vực nhỏ nên về cơ bản chúng ta có thể giảm lượng tần số và mắt người sẽ không thể nhận ra sự khác biệt. Kết quả? Một hình ảnh được nén ở mức độ cao mà hầu như không bị giảm chất lượng.
Giống như mỗi pixel trong không gian màu RGB được tạo thành từ 3 byte dữ liệu màu (Đỏ, Xanh lục, Xanh lam), mỗi pixel trong YUV cũng sử dụng 3 byte nhưng nội dung mà mỗi byte biểu thị hơi khác nhau. Thành phần Y xác định độ sáng của màu (còn được gọi là độ chói hoặc độ sáng), trong khi thành phần U và V xác định màu (còn được gọi là sắc độ). Thành phần U đề cập đến lượng màu xanh lam và thành phần V đề cập đến lượng màu đỏ.
Định dạng màu này được phát minh khi TV màu chưa phổ biến và các kỹ sư muốn sử dụng một định dạng mã hóa hình ảnh cho cả TV màu và TV đen trắng. YUV có thể được hiển thị an toàn trên TV đen trắng nếu không có màu. Bạn có thể đọc thêm về lịch sử của nó trên Wikipedia.
Biến đổi và lượng tử hóa cosine rời rạc
JPEG chuyển đổi một hình ảnh thành các khối pixel 8x8 (được gọi là MCU hoặc Đơn vị mã hóa tối thiểu), thay đổi phạm vi giá trị của các pixel để chúng tập trung vào 0 và sau đó áp dụng Chuyển đổi Cosine rời rạc cho từng khối và sau đó sử dụng lượng tử hóa để nén khối kết quả. Chúng ta hãy hiểu ở mức độ cao hơn về ý nghĩa của tất cả các thuật ngữ này.
Biến đổi Cosine rời rạc là một phương pháp chuyển đổi các điểm dữ liệu rời rạc thành sự kết hợp của các sóng cosine. Có vẻ khá vô ích khi dành thời gian chuyển đổi một hình ảnh thành một loạt cos nhưng sẽ có ý nghĩa khi chúng ta hiểu DCT kết hợp với cách hoạt động của bước tiếp theo. Trong JPEG, DCT sẽ lấy một khối hình ảnh 8x8 và cho chúng ta biết cách tái tạo nó bằng ma trận 8x8 gồm các hàm cosine. Đọc thêm tại đây)
Ma trận 8x8 của hàm cosine trông như thế này:

Chúng tôi áp dụng DCT cho từng thành phần của pixel một cách riêng biệt. Đầu ra của việc áp dụng DCT là một ma trận hệ số 8x8 cho chúng ta biết mỗi hàm cosine (trong tổng số 64 hàm) đóng góp bao nhiêu vào ma trận đầu vào 8x8. Ma trận hệ số của DCT thường chứa các giá trị lớn hơn ở góc trên bên trái của ma trận hệ số và các giá trị nhỏ hơn ở góc dưới bên phải. Góc trên bên trái biểu thị hàm cosin tần số thấp nhất và góc dưới bên phải biểu thị hàm cosin tần số cao nhất.
Điều này cho chúng ta biết rằng hầu hết các hình ảnh đều chứa một lượng lớn thông tin tần số thấp và một lượng nhỏ thông tin tần số cao. Nếu chúng ta chuyển các thành phần dưới cùng bên phải của mỗi ma trận DCT về 0, hình ảnh thu được vẫn xuất hiện giống nhau vì như tôi đã đề cập, con người rất kém trong việc quan sát những thay đổi tần số cao. Đây chính xác là những gì chúng ta làm trong bước tiếp theo.
Tất cả chúng ta đều đã nghe nói rằng JPEG là một thuật toán nén có tổn hao nhưng cho đến nay chúng ta vẫn chưa thực hiện bất kỳ thuật toán nào có tổn hao. Chúng tôi chỉ chuyển đổi các khối thành phần YUV 8x8 thành các khối hàm cosin 8x8 mà không làm mất thông tin. Phần mất mát xuất hiện trong bước lượng tử hóa.
Lượng tử hóa là một quá trình trong đó chúng ta lấy một vài giá trị trong một phạm vi cụ thể và biến chúng thành một giá trị riêng biệt. Đối với trường hợp của chúng tôi, đây chỉ là một cái tên ưa thích để chuyển đổi các hệ số tần số cao hơn trong ma trận đầu ra DCT thành 0. Khi bạn lưu hình ảnh bằng JPEG, hầu hết các chương trình chỉnh sửa hình ảnh đều hỏi bạn cần nén bao nhiêu. Tỷ lệ phần trăm bạn cung cấp ở đó ảnh hưởng đến mức độ lượng tử hóa được áp dụng và lượng thông tin tần số cao hơn bị mất. Đây là nơi áp dụng nén mất mát. Khi bạn mất thông tin tần số cao, bạn không thể tạo lại hình ảnh gốc chính xác từ hình ảnh JPEG thu được.
Tùy thuộc vào mức độ nén được yêu cầu, một số ma trận lượng tử hóa phổ biến sẽ được sử dụng (sự thật thú vị: Hầu hết các nhà cung cấp đều có bằng sáng chế về xây dựng bảng lượng tử hóa). Chúng tôi chia phần tử ma trận hệ số DCT với ma trận lượng tử hóa, làm tròn kết quả thành một số nguyên và lấy ma trận lượng tử hóa. Hãy xem qua một ví dụ.
Nếu bạn có ma trận DCT này:

Ma trận lượng tử hóa (phổ biến) này:
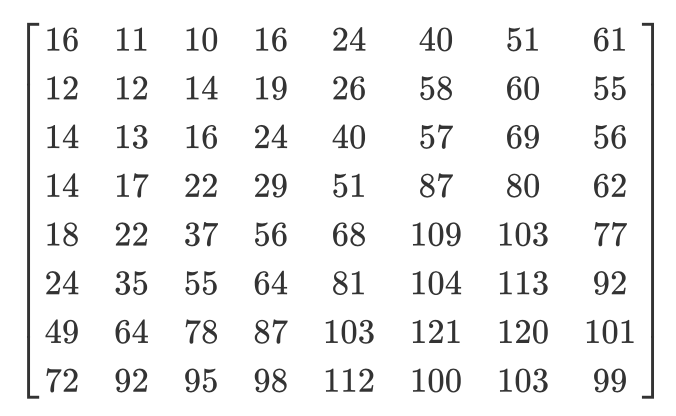
Sau đó, ma trận lượng tử hóa kết quả sẽ là:

Mặc dù con người không thể nhìn thấy thông tin tần số cao nhưng nếu bạn loại bỏ quá nhiều thông tin khỏi các khối hình ảnh 8x8 thì hình ảnh tổng thể sẽ trông có vẻ khối. Trong ma trận lượng tử hóa này, giá trị đầu tiên được gọi là giá trị DC và các giá trị còn lại là giá trị AC. Nếu chúng ta lấy các giá trị DC từ tất cả các ma trận lượng tử hóa và tạo ra một hình ảnh mới, về cơ bản chúng ta sẽ có một hình thu nhỏ có độ phân giải bằng 1/8 của hình ảnh gốc.
Cũng cần lưu ý rằng vì chúng tôi áp dụng lượng tử hóa trong khi giải mã nên chúng tôi sẽ phải đảm bảo màu sắc nằm trong phạm vi [0,255]. Nếu chúng nằm ngoài phạm vi này, chúng ta sẽ phải kẹp chúng vào phạm vi này theo cách thủ công.
Zig-zag
Sau khi lượng tử hóa, JPEG sử dụng mã hóa zig-zag để chuyển đổi ma trận thành 1D (img src):
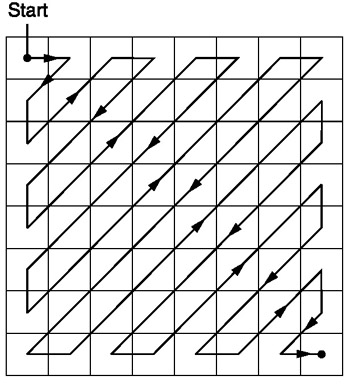
Hãy tưởng tượng chúng ta có ma trận lượng tử hóa này:
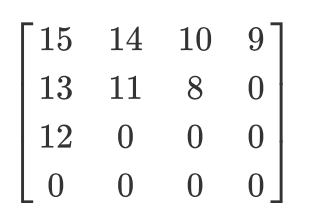
Đầu ra của mã hóa zig-zag sẽ là:
[15 14 13 12 11 10 9 8 0 … 0]
Mã hóa này được ưu tiên vì hầu hết thông tin tần số thấp (quan trọng nhất) được lưu trữ ở đầu ma trận sau khi lượng tử hóa và mã hóa zig-zag lưu trữ tất cả thông tin đó ở đầu ma trận 1D. Điều này rất hữu ích cho việc nén xảy ra ở bước tiếp theo.
Mã hóa độ dài chạy và Delta
Mã hóa độ dài chạy được sử dụng để nén dữ liệu lặp lại. Khi kết thúc quá trình mã hóa zig-zag, chúng ta thấy hầu hết các mảng 1D được mã hóa zig-zag đều có rất nhiều số 0 ở cuối. Mã hóa độ dài thời gian chạy cho phép chúng tôi lấy lại tất cả không gian bị lãng phí đó và sử dụng ít byte hơn để biểu thị tất cả các số 0 đó. Hãy tưởng tượng bạn có một số dữ liệu như thế này:
10 10 10 10 10 10 10
Mã hóa độ dài chạy sẽ chuyển đổi nó thành:
7 10
Chúng tôi đã có thể nén thành công 7 byte dữ liệu thành 2 byte.
Mã hóa Delta là một kỹ thuật được sử dụng để biểu diễn một byte so với byte trước nó. Điều này dễ hiểu hơn bằng một ví dụ. Giả sử bạn có dữ liệu sau:
10 11 12 13 10 9
Bạn có thể sử dụng mã hóa delta để lưu trữ nó như thế này:
10 1 2 3 0 -1
Trong JPEG, mọi giá trị DC trong ma trận hệ số DCT được mã hóa delta so với giá trị DC trước nó. Điều này có nghĩa là nếu bạn thay đổi hệ số DCT đầu tiên của hình ảnh, toàn bộ hình ảnh sẽ bị sai lệch nhưng nếu bạn sửa đổi giá trị đầu tiên của ma trận DCT cuối cùng thì chỉ một phần rất nhỏ trong hình ảnh của bạn sẽ bị ảnh hưởng. Điều này rất hữu ích vì giá trị DC đầu tiên trong hình ảnh của bạn thường đa dạng nhất và bằng cách áp dụng mã hóa Delta, chúng tôi đưa các giá trị DC còn lại về gần 0 và điều đó dẫn đến khả năng nén tốt hơn trong bước tiếp theo của Mã hóa Huffman.
Huffman Encoding
Mã hóa Huffman là một phương pháp nén thông tin không mất dữ liệu. Huffman từng tự hỏi: “Tôi có thể sử dụng bao nhiêu bit nhỏ nhất để lưu trữ một đoạn văn bản tùy ý?”. Định dạng mã hóa này là câu trả lời của anh ấy. Hãy tưởng tượng bạn phải lưu trữ văn bản này:
a b c d e
Trong trường hợp bình thường, mỗi ký tự sẽ chiếm 1 byte dung lượng:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
Điều này dựa trên ASCII để ánh xạ nhị phân. Nhưng điều gì sẽ xảy ra nếu chúng ta có thể tạo ra một bản đồ tùy chỉnh?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Bây giờ chúng ta có thể lưu trữ cùng một văn bản bằng cách sử dụng ít bit hơn:
a: 000
b: 001
c: 010
d: 100
e: 011
Điều này hoàn toàn tốt nhưng nếu chúng ta muốn chiếm ít không gian hơn thì sao? Điều gì sẽ xảy ra nếu chúng ta có thể làm được điều gì đó như thế này:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
Mã hóa Huffman cho phép chúng ta sử dụng loại ánh xạ có độ dài thay đổi này. Nó lấy một số dữ liệu đầu vào, ánh xạ các ký tự thường xuyên nhất sang các mẫu bit nhỏ hơn và các ký tự ít thường xuyên nhất thành các mẫu bit lớn hơn và cuối cùng tổ chức ánh xạ thành cây nhị phân. Trong JPEG, chúng tôi lưu trữ thông tin DCT (Biến đổi Cosine rời rạc) bằng cách sử dụng mã hóa Huffman. Hãy nhớ rằng tôi đã nói với bạn rằng việc sử dụng mã hóa delta cho các giá trị DC sẽ giúp ích cho Mã hóa Huffman? Tôi hy vọng bây giờ bạn có thể hiểu tại sao. Sau khi mã hóa delta, chúng tôi thu được ít “ký tự” hơn để ánh xạ và tổng kích thước của cây Huffman của chúng tôi giảm xuống.
Tom Scott có một video tuyệt vời kèm theo hình ảnh động về cách hoạt động của mã hóa Huffman nói chung. Hãy xem nó trước khi tiếp tục.
Một JPEG chứa tối đa 4 bảng Huffman và những bảng này được lưu trữ trong phần “Xác định bảng Huffman” (bắt đầu bằng 0xffc4). Các hệ số DCT được lưu trữ trong 2 bảng Huffman khác nhau. Một cái chỉ chứa các giá trị DC từ các bảng zig-zag và cái kia chứa các giá trị AC từ các bảng zig-zag. Điều này có nghĩa là trong quá trình giải mã, chúng ta sẽ phải hợp nhất các giá trị DC và AC từ hai ma trận riêng biệt. Thông tin DCT cho kênh độ chói và sắc độ được lưu trữ riêng biệt nên chúng ta có 2 bộ thông tin DC và 2 bộ thông tin AC, cung cấp cho chúng ta tổng cộng 4 bảng Huffman.
Trong ảnh thang độ xám, chúng ta sẽ chỉ có 2 bảng Huffman (1 cho DC và 1 cho AC) vì chúng ta không quan tâm đến màu sắc. Như bạn có thể tưởng tượng, 2 hình ảnh có thể có các bảng Huffman rất khác nhau nên điều quan trọng là phải lưu trữ các bảng này bên trong mỗi JPEG.
Vì vậy, chúng tôi biết các chi tiết cơ bản về nội dung của hình ảnh JPEG. Hãy bắt đầu với việc giải mã!
Giải mã JPEG
Chúng ta có thể chia quá trình giải mã thành nhiều bước:
- Trích xuất bảng Huffman và giải mã các bit
- Trích xuất các hệ số DCT bằng cách hoàn tác mã hóa độ dài chạy và delta
- Sử dụng hệ số DCT để kết hợp sóng cosine và tái tạo giá trị pixel cho mỗi khối 8x8
- Chuyển đổi YCbCr sang RGB cho mỗi pixel
- Hiển thị hình ảnh RGB thu được
Chuẩn JPEG hỗ trợ 4 định dạng nén:
- Đường cơ sở
- Trình tự mở rộng
- Cấp tiến
- Không mất mát
Chúng ta sẽ làm việc với tính năng nén Đường cơ sở và theo tiêu chuẩn, đường cơ sở sẽ chứa một chuỗi các khối 8x8 ngay cạnh nhau. Các định dạng nén khác bố trí dữ liệu hơi khác một chút. Chỉ để tham khảo, tôi đã tô màu các phân đoạn khác nhau trong nội dung hex của hình ảnh mà chúng tôi đang sử dụng. Cái này nó thì trông như thế nào:
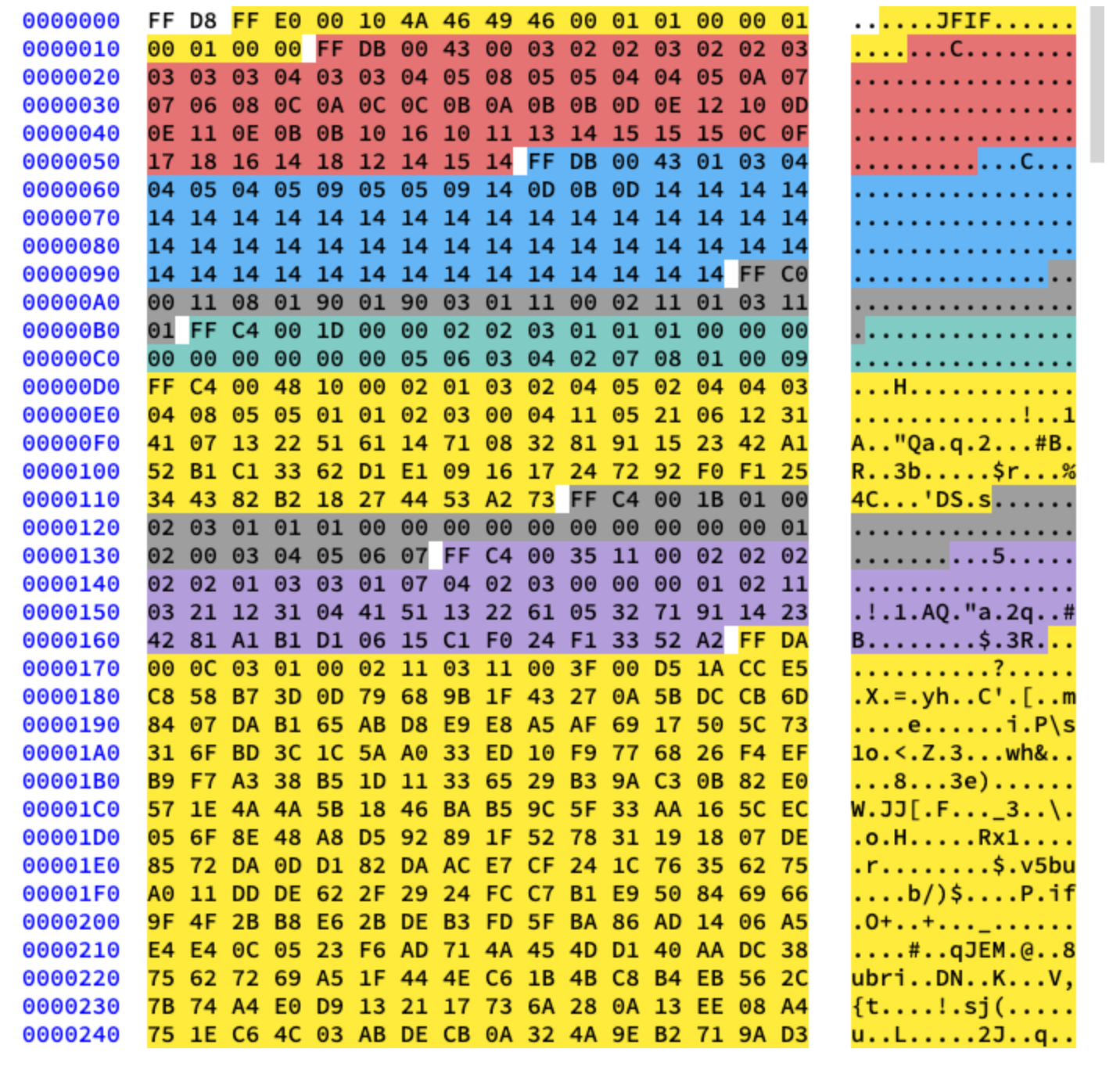
Trích xuất bảng Huffman
Chúng ta đã biết rằng một JPEG chứa 4 bảng Huffman. Đây là bước cuối cùng trong quy trình mã hóa nên phải là bước đầu tiên trong quy trình giải mã. Mỗi phần DHT chứa các thông tin sau:
| Field | Size | Description |
|---|---|---|
| Marker Identifier | 2 bytes | 0xff, 0xc4 để xác định điểm đánh dấu DHT |
| Length | 2 bytes | Điều này chỉ định độ dài của bảng Huffman |
| HT information | 1 byte | bit 0..3: number of HT (0..3, otherwise error). bit 4: type of HT, 0 = DC table, 1 = AC table. bit 5..7: not used, must be 0 |
| Number of Symbols | 16 bytes | Số ký hiệu có mã có độ dài 1..16, tổng (n) của các byte này là tổng số mã, phải <= 256 |
| Symbols | n bytes | Bảng chứa các ký hiệu theo thứ tự độ dài mã tăng dần ( n = tổng số mã ). |
Giả sử bạn có bảng DH tương tự như thế này (src):
| Symbol | Huffman code | Code length |
|---|---|---|
| a | 00 | 2 |
| b | 010 | 3 |
| c | 011 | 3 |
| d | 100 | 3 |
| e | 101 | 3 |
| f | 110 | 3 |
| g | 1110 | 4 |
| h | 11110 | 5 |
| i | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| l | 111111110 | 9 |
Nó sẽ được lưu trữ trong tệp JFIF gần như thế này (chúng sẽ được lưu ở dạng nhị phân. Tôi đang sử dụng ASCII chỉ nhằm mục đích minh họa):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
Số 0 có nghĩa là không có mã Huffman có độ dài 1. 1 có nghĩa là có 1 mã Huffman có độ dài 2, v.v. Luôn có 16 byte dữ liệu có độ dài trong phần DHT ngay sau thông tin lớp và ID. Hãy viết một số mã để trích xuất độ dài và các phần tử trong DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Nếu bạn chạy mã, nó sẽ tạo ra kết quả sau:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
Tuyệt! Chúng ta đã có độ dài và các phần tử. Bây giờ chúng ta cần tạo một lớp bảng Huffman tùy chỉnh để có thể tạo lại cây nhị phân từ các phần tử và độ dài này. Tôi đang sao chép mã này một cách đáng xấu hổ từ đây:
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBits lấy độ dài và phần tử, lặp lại tất cả các phần tử và đặt chúng vào danh sách gốc. Danh sách này chứa các danh sách lồng nhau và thể hiện một cây nhị phân. Bạn có thể đọc trực tuyến về cách hoạt động của Cây Huffman và cách tạo cấu trúc dữ liệu cây Huffman của riêng bạn bằng Python. Đối với DHT đầu tiên của chúng tôi (sử dụng hình ảnh tôi đã liên kết ở đầu hướng dẫn này), chúng tôi có dữ liệu, độ dài và thành phần sau:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00 Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0) Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
Sau khi gọi GetHuffmanBits về điều này, danh sách gốc root sẽ chứa dữ liệu này:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTable cũng chứa phương thức GetCode để duyệt cây cho chúng ta và trả lại cho chúng ta các bit đã được giải mã bằng bảng Huffman. Phương pháp này yêu cầu dòng bit làm đầu vào. Dòng bit chỉ là biểu diễn nhị phân của dữ liệu. Ví dụ: dòng bit điển hình của abc sẽ là 011000010110001001100011. Trước tiên, chúng tôi chuyển đổi từng ký tự thành mã ASCII của nó và sau đó chuyển đổi mã ASCII đó thành nhị phân. Hãy tạo một lớp tùy chỉnh cho phép chúng ta chuyển đổi một chuỗi thành các bit và đọc từng bit một. Đây là cách chúng tôi sẽ thực hiện nó:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
Chúng tôi cung cấp cho lớp này một số dữ liệu nhị phân trong khi khởi tạo nó và sau đó sử dụng các phương thức GetBit và GetBitN để đọc nó.
Giải mã bảng lượng tử hóa
Phần Bảng lượng tử hóa xác định chứa dữ liệu sau:
| Field | Size | Description |
|---|---|---|
| Marker Identifier | 2 bytes | 0xff, 0xdb xác định DQT |
| Length | 2 bytes | Điều này cho biết độ dài của QT. |
| QT information | 1 byte | bit 0..3: number of QT (0..3, otherwise error) bit 4..7: the precision of QT, 0 = 8 bit, otherwise 16 bit |
| Bytes | n bytes | Điều này mang lại giá trị QT, n = 64*(precision+1) |
Theo tiêu chuẩn JPEG, có 2 bảng lượng tử hóa mặc định trong một ảnh JPEG. Một cho độ chói và một cho sắc độ. Các bảng này bắt đầu ở điểm đánh dấu 0xffdb. Trong mã ban đầu mà chúng tôi viết, chúng tôi đã thấy rằng đầu ra chứa hai điểm đánh dấu 0xffdb. Hãy mở rộng mã mà chúng ta đã có và thêm khả năng giải mã các bảng lượng tử hóa:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Chúng tôi đã làm một vài điều ở đây. Đầu tiên, tôi định nghĩa phương thức GetArray. Nó chỉ là một phương pháp hữu ích để giải mã số byte thay đổi từ dữ liệu nhị phân. Tôi đã thay thế một số mã trong phương thức giải decodeHuffman để tận dụng chức năng mới này. Sau đó, tôi đã xác định phương thức DefinQuantizationTables. Phương pháp này chỉ cần đọc tiêu đề của phần Bảng lượng tử hóa và sau đó nối thêm dữ liệu lượng tử hóa vào từ điển với giá trị tiêu đề làm khóa. Giá trị tiêu đề sẽ là 0 cho độ sáng và 1 cho màu sắc. Mỗi phần Bảng lượng tử hóa trong JFIF chứa 64 byte dữ liệu QT (đối với ma trận Lượng tử hóa 8x8 của chúng tôi).
Nếu chúng ta in ma trận lượng tử hóa cho hình ảnh của mình. Chúng sẽ trông như thế này:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Giải mã bắt đầu khung
Phần Bắt đầu Khung chứa thông tin sau (src):
| Field | Size | Description |
|---|---|---|
| Marker Identifier | 2 bytes | 0xff, 0xc0 để xác định điểm đánh dấu SOF0 |
| Length | 2 bytes | Giá trị này bằng giá trị 8 + components*3 |
| Data precision | 1 byte | Đây là bit/mẫu, thường là 8 (12 và 16 không được hầu hết các phần mềm hỗ trợ). |
| Image height | 2 bytes | Giá trị này phải > 0 |
| Image Width | 2 bytes | Giá trị này phải > 0 |
| Number of components | 1 byte | Thông thường 1 = thang màu xám, 3 = màu YcbCr hoặc YIQ |
| Each component | 3 bytes | Đọc từng dữ liệu thành phần 3 byte. Nó chứa, (Id thành phần (1byte)(1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), hệ số lấy mẫu (1byte) (bit 0-3 dọc, 4-7 ngang.) , số bảng lượng tử hóa (1 byte)). |
Trong số dữ liệu này, chúng tôi chỉ quan tâm đến một số điều. Chúng tôi sẽ trích xuất chiều rộng và chiều cao của hình ảnh và số bảng lượng tử hóa của từng thành phần. Chiều rộng và chiều cao sẽ được sử dụng khi chúng ta bắt đầu giải mã các bản quét hình ảnh thực tế từ phần Bắt đầu quét. Vì chúng ta chủ yếu làm việc với hình ảnh YCbCr nên chúng ta có thể mong đợi số lượng thành phần bằng 3 và các loại thành phần tương ứng bằng 1, 2 và 3. Hãy viết một số mã để giải mã dữ liệu này:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Chúng tôi đã thêm thuộc tính danh sách quantMapping vào lớp JPEG của mình và giới thiệu phương pháp BaselineDCT. Phương thức BaselineDCT giải mã dữ liệu cần thiết từ phần SOF và đặt số bảng lượng tử hóa của từng thành phần vào danh sách quantMapping. Chúng tôi sẽ sử dụng ánh xạ này khi chúng tôi bắt đầu đọc phần Bắt đầu quét. quantMapping trông như thế này đối với hình ảnh của chúng ta:
Quant mapping: [0, 1, 1]
Giải mã Bắt đầu quét
Tuyệt! Chúng ta chỉ còn một phần nữa để giải mã. Đây là phần cốt lõi của hình ảnh JPEG và chứa dữ liệu “hình ảnh” thực tế. Đây cũng là bước liên quan nhiều nhất. Mọi thứ khác mà chúng tôi đã giải mã cho đến nay có thể được coi là việc tạo bản đồ để giúp chúng tôi điều hướng và giải mã hình ảnh thực tế. Phần này chứa hình ảnh thực tế (mặc dù ở dạng được mã hóa). Chúng ta sẽ đọc phần này và sử dụng dữ liệu đã giải mã để hiểu được hình ảnh.
Tất cả các điểm đánh dấu mà chúng ta đã thấy cho đến nay đều bắt đầu bằng 0xff. 0xff cũng có thể là một phần của dữ liệu quét hình ảnh nhưng nếu 0xff có trong dữ liệu quét, nó sẽ luôn được xử lý theo 0x00. Đây là điều mà bộ mã hóa JPEG thực hiện tự động và được gọi là nhồi byte. Nhiệm vụ của bộ giải mã là loại bỏ thủ tục 0x00 này. Hãy bắt đầu phương thức giải mã SOS với chức năng này và loại bỏ 0x00 nếu có. Trong hình ảnh mẫu tôi đang sử dụng, chúng tôi không có 0xff trong dữ liệu quét hình ảnh nhưng đây vẫn là một bổ sung hữu ích.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Trước đây, tôi đã tìm kiếm thủ công đến cuối tệp bất cứ khi nào tôi gặp điểm đánh dấu 0xffda nhưng bây giờ chúng tôi đã có sẵn công cụ cần thiết để xem qua toàn bộ tệp theo thứ tự có hệ thống, tôi đã di chuyển điều kiện đánh dấu bên trong mệnh đề else. Hàm RemoveFF00 chỉ đơn giản là ngắt bất cứ khi nào nó quan sát thấy thứ gì đó khác 0x00 sau 0xff. Do đó, nó sẽ thoát ra khỏi vòng lặp khi gặp 0xffd9 và bằng cách đó chúng ta có thể tìm kiếm đến cuối tệp một cách an toàn mà không có bất kỳ sự ngạc nhiên nào. Nếu bạn chạy mã này ngay bây giờ, sẽ không có gì mới xuất ra thiết bị đầu cuối.
Hãy nhớ lại rằng JPEG đã chia hình ảnh thành ma trận 8x8. Bước tiếp theo của chúng tôi là chuyển đổi dữ liệu quét hình ảnh thành luồng bit và xử lý luồng đó theo khối dữ liệu 8x8. Hãy thêm một số mã nữa vào lớp của chúng ta:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Chúng tôi bắt đầu bằng cách chuyển đổi dữ liệu quét của mình thành luồng bit. Sau đó, chúng ta khởi tạo oldlumdccoeff, oldCbdccoeff, oldCrdccoeff thành 0. Những điều này là bắt buộc vì bạn có nhớ chúng ta đã nói về cách phần tử DC trong ma trận lượng tử hóa (phần tử đầu tiên của ma trận) được mã hóa delta so với phần tử DC trước đó không? Điều này sẽ giúp chúng ta theo dõi giá trị của các phần tử DC trước đó và 0 sẽ là mặc định khi chúng ta gặp phần tử DC đầu tiên.
Vòng lặp for có vẻ hơi thú vị. self.height//8 cho chúng ta biết chúng ta có thể chia chiều cao cho 8 bao nhiêu lần. Điều tương tự cũng xảy ra với self.width//8. Tóm lại, điều này cho chúng ta biết hình ảnh được chia thành bao nhiêu ma trận 8x8.
BuildMatrix sẽ lấy bảng lượng tử hóa và một số thông số bổ sung, tạo Ma trận biến đổi Cosine rời rạc nghịch đảo và cung cấp cho chúng ta các ma trận Y, Cr và Cb. Việc chuyển đổi thực tế các ma trận này sang RGB sẽ diễn ra trong hàm DrawMatrix.
Trước tiên, hãy tạo lớp IDCT và sau đó chúng ta có thể bắt đầu phát triển phương thức BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Chúng ta hãy cố gắng hiểu lớp IDCT này từng bước một. Khi chúng tôi trích xuất MCU từ JPEG, thuộc tính cơ sở của lớp này sẽ lưu trữ nó. Sau đó chúng ta sẽ sắp xếp lại ma trận MCU bằng cách hoàn tác mã hóa zigzag thông qua phương thức rearrange_using_zigzag. Cuối cùng, chúng ta sẽ hoàn tác Chuyển đổi Cosine rời rạc bằng cách gọi phương thức performance_IDCT.
Nếu bạn còn nhớ thì bảng Cosine rời rạc đã được sửa. Cách tính toán thực tế cho DCT nằm ngoài phạm vi của hướng dẫn này vì nó thiên về toán học hơn là lập trình. Chúng ta có thể lưu trữ bảng này dưới dạng biến toàn cục và sau đó truy vấn bảng đó để tìm các giá trị dựa trên cặp x, y. Tôi quyết định đặt bảng và phép tính của nó vào lớp IDCT để dễ đọc. Mỗi phần tử của ma trận MCU được sắp xếp lại sẽ được nhân với các giá trị của idc_variable và cuối cùng chúng ta nhận được các giá trị Y, Cr và Cb.
Điều này sẽ có ý nghĩa hơn khi chúng ta viết ra phương thức BuildMatrix.
Nếu bạn sửa đổi bảng ngoằn ngoèo thành một cái gì đó như thế này:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
Bạn sẽ có kết quả đầu ra sau (chú ý các hiện vật nhỏ):

Và nếu bạn dũng cảm hơn nữa, bạn có thể sửa đổi bảng ngoằn ngoèo hơn nữa:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Nó sẽ dẫn đến kết quả đầu ra này:

Bây giờ hãy hoàn thành phương thức BuildMatrix của chúng ta:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Chúng tôi bắt đầu bằng cách tạo một lớp Biến đổi Cosine rời rạc nghịch đảo (IDCT()). Sau đó, chúng tôi đọc dòng bit và giải mã nó bằng bảng Huffman.
self.huffman_tables[0] và self.huffman_tables[1] lần lượt đề cập đến các bảng DC về độ chói và sắc độ, còn self.huffman_tables[16] và self.huffman_tables[17] lần lượt đề cập đến các bảng AC về độ chói và sắc độ.
Sau khi giải mã dòng bit, chúng tôi trích xuất hệ số DC được mã hóa delta mới bằng cách sử dụng hàm DecodeNumber và thêm hệ số olddccofactor vào đó để có được hệ số DC được giải mã delta.
Sau đó, chúng tôi lặp lại quy trình giải mã tương tự nhưng đối với các giá trị AC trong ma trận lượng tử hóa. Giá trị mã bằng 0 gợi ý rằng chúng tôi đã gặp phải điểm đánh dấu Kết thúc khối (EOB) và chúng tôi cần dừng lại. Hơn nữa, phần đầu tiên của bảng lượng tử AC cho chúng ta biết chúng ta có bao nhiêu số 0 đứng đầu. Bạn còn nhớ cách mã hóa độ dài chạy mà chúng ta đã nói đến ở phần đầu tiên không? Đây là lúc điều đó đang phát huy tác dụng. Chúng tôi giải mã mã hóa độ dài chạy và bỏ qua nhiều bit đó. Tất cả các bit bị bỏ qua đều được đặt thành 0 trong lớp IDCT.
Sau khi giải mã xong các giá trị DC và AC cho MCU, chúng tôi sắp xếp lại MCU và hoàn tác mã hóa zigzag bằng cách gọi rearrange_using_zigzag, sau đó chúng tôi thực hiện DCT nghịch đảo trên MCU đã giải mã.
Phương thức BuildMatrix sẽ trả về ma trận DCT nghịch đảo và giá trị của hệ số DC. Hãy nhớ rằng, ma trận DCT nghịch đảo này chỉ dành cho một ma trận MCU (Đơn vị mã hóa tối thiểu) 8x8 nhỏ. Chúng tôi sẽ thực hiện việc này cho tất cả các MCU riêng lẻ trong toàn bộ tệp hình ảnh.
Hiển thị hình ảnh trên màn hình
Hãy sửa đổi mã của chúng tôi một chút và tạo Tkinter Canvas và vẽ từng MCU sau khi giải mã nó theo phương thức StartOfScan.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Hãy bắt đầu với các hàm ColorConversion và Clamp . ColorConversion nhận các giá trị Y, Cr và Cb, sử dụng công thức để chuyển đổi các giá trị này thành các giá trị tương ứng RGB của chúng, sau đó xuất ra các giá trị RGB được kẹp. Bạn có thể thắc mắc tại sao chúng tôi lại thêm 128 vào giá trị RGB. Nếu bạn còn nhớ, trước khi máy nén JPEG áp dụng DCT trên MCU, nó sẽ trừ 128 khỏi giá trị màu. Nếu màu ban đầu nằm trong phạm vi [0,255] thì JPEG sẽ đặt chúng vào phạm vi [-128,+128]. Vì vậy, chúng tôi phải hoàn tác hiệu ứng đó khi giải mã JPEG và đó là lý do tại sao chúng tôi thêm 128 vào RGB. Đối với Clamp, trong quá trình giải nén, giá trị đầu ra có thể vượt quá [0,255] nên chúng tôi kẹp chúng trong khoảng [0,255] .
Trong phương thức DrawMatrix, chúng tôi lặp qua từng ma trận Y, Cr và Cb được giải mã 8x8 và chuyển đổi từng phần tử của ma trận 8x8 thành các giá trị RGB. Sau khi chuyển đổi, chúng tôi vẽ từng pixel trên canvas Tkinter bằng phương thức create_ectangle. Bạn có thể tìm thấy mã hoàn chỉnh trên GitHub. Bây giờ nếu bạn chạy mã này, khuôn mặt của tôi sẽ hiển thị trên màn hình của bạn 😄
Tổng kết
Oh Boy! Ai có thể nghĩ rằng sẽ phải mất hơn 6000 từ + lời giải thích để hiển thị khuôn mặt của tôi trên màn hình. Tôi ngạc nhiên trước sự thông minh của một số nhà phát minh thuật toán này! Tôi hy vọng bạn thích bài viết này cũng như tôi thích viết nó. Tôi đã học được rất nhiều điều khi viết bộ giải mã này. Tôi chưa bao giờ nhận ra rằng việc mã hóa một hình ảnh JPEG đơn giản lại phức tạp đến mức nào. Tiếp theo tôi có thể làm việc trên hình ảnh PNG và thử viết bộ giải mã cho hình ảnh PNG. Bạn cũng nên thử viết bộ giải mã cho PNG (hoặc một số định dạng khác). Tôi chắc chắn rằng nó sẽ đòi hỏi rất nhiều điều để học hỏi và thậm chí còn nhiều điều thú vị hơn nữa 😅
Dù thế nào đi nữa, bây giờ tôi cũng mệt rồi. Tôi đã nhìn chằm chằm vào hex quá lâu và tôi nghĩ rằng mình đã có được một kỳ nghỉ xứng đáng. Tất cả các bạn hãy cẩn thận và nếu bạn có bất kỳ câu hỏi nào, vui lòng viết chúng trong phần bình luận bên dưới. Tôi là người mới tham gia cuộc phiêu lưu mã hóa JPEG này nhưng tôi sẽ cố gắng trả lời nhiều nhất có thể 😄
Tạm biệt! 👋 ❤️
Đọc thêm
Nếu bạn muốn đi sâu vào chi tiết hơn, bạn có thể xem qua một số tài liệu tôi đã sử dụng khi viết bài viết này. Tôi cũng đã thêm một số liên kết bổ sung cho một số nội dung thú vị liên quan đến JPEG:
- An illustrated guide to Unraveling the JPEG
- An extremely detailed article on JPEG Huffman Coding
- Let’s write a simple JPEG library. Uses C++
- Python 3 struct documentation
- Read this article on how FB used this knowledge about JPEG
- JPEG File layout and format
- An interesting presentation by Department of Defense on JPEG forensics
Tham khảo:
- Decoding binary data structure
- Understanding and Decoding a JPEG Image using Python
- DCode™ – Timestamp Decoder
- 图片的 Metadata 与网站性能优化
- Báo cáo và CODE nén ảnh JPEG